티스토리 뷰
안녕하세요 SweetDev입니다. 저는 지금 컴공 2학년 수업인 자료구조에서 트리를 배우는 중이라고 해서(사실 수업 잘 안가서 모름) 시험공부도 미리 할 겸 트리를 정리해보려고 합니다!
1. 정의
트리 : hierarchy구조의 데이터를 표현하기 위한 자료 구조
2. 트리를 표현하기 위해서 쓰는 단어들
- Node
- Root Node
- Child Node , Children
- degree, fan out
- Sibling
- Ancestor
- Descendant
- Leaf node, Leaves,
- Non-Leaf Node
- Subtree
- Forest
- Path from node x to node y
- Level
- 0, 1, 2, ~ h-1
- 1, 2, 3, ~ h
- Height : max, level
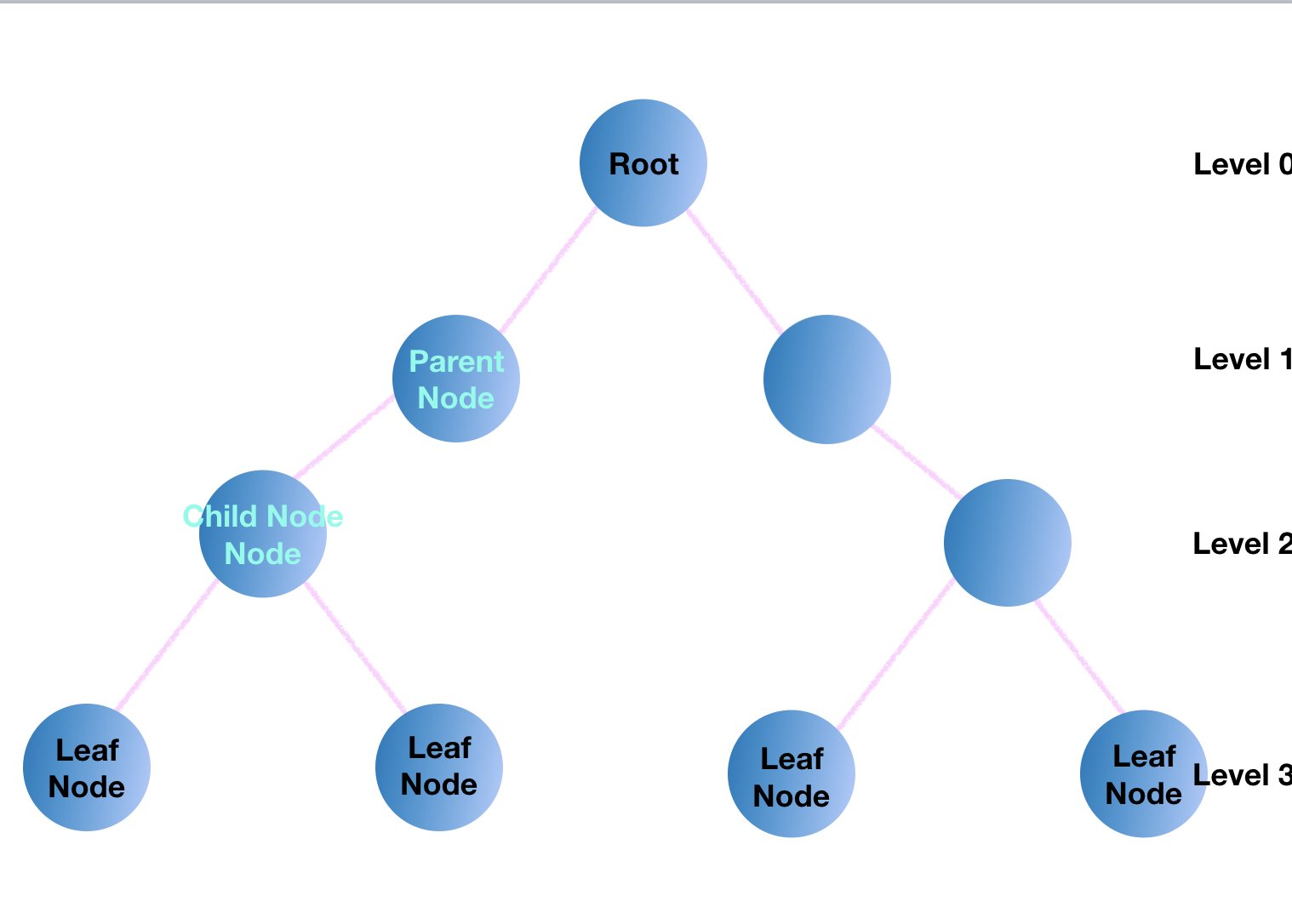
이런 단어들을 배울 예정이라고 하네용
사실 이산수학때 트리에 대해서 나름? 자세하게 배워서 어느정도 알기는 하지만..! 꼼꼼하게 정리해보는거루..ㅎ
이제 Binary Tree, Full, Complete, Skewed에 대해서 얘기해용!!
3. Binary Tree
이름처럼, 각 노드가 최대 2개까지 자식을 가질 수 있는 트리.
자식이 두개밖에 없으니까 Left Node, Right Node 이런식으로 이름을 붙인다고 합니다.
Subtree도 간단하게 Left Subtree, Right Subtree!
4. Full Binary Tree
Ful! 꽉 찼다는 뜻이지...!
Leaf Node를 제외하고, 모든 노드가 2개씩 자식을 갖고 있는 형태에요
Leaf Node는 제일 마지막에 있는, '잎'같은 노드입니다
위에 있는 그림 참조하세용
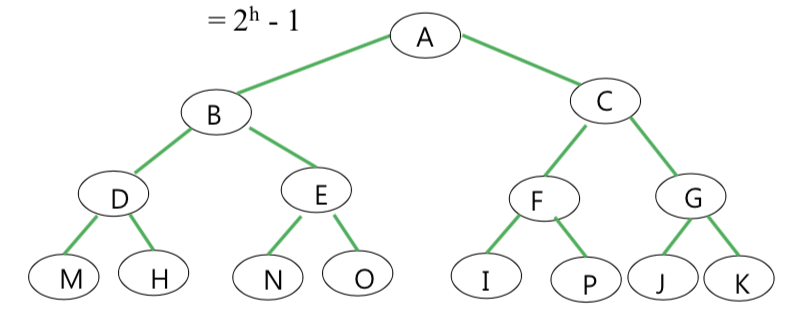
Full Binary Tree의 높이는 , 전체 노드 갯수가 n일 때, 그리고 leaf node 개수가 n0일 때
- height = log2(n+1)
- height = log2(n0) + 1
왜냐면 노드 1개면 height = 1
노드 3개면 height = 2
노드 7개면 height = 3
이런식으로 되기 때문이지!
막줄 갯수 * 2 하면 (전체 노드 개수 -1 )이기 때문에 저게 성립하기도 하구!1
5. Complete Binary Tree
Full이랑 이름이 비슷해서 헷깔리기 쉽지만!
Complete Binary Tree는

이런 모양이라고 설명하는데,
가장 밑에줄 보다 하나 위까지는 full 트리이지만, 마지막줄이 full이 아닐 수 있고 오른쪽 노드부터 몇개가 없는거라고 하네요........>!!!!!!!
개신기.........
height이 h일 때,
max는 맨 밑에줄이 꽉 차있는 1 + 2 + 4 + 8 + ... + 2^(h-1)이니까 2^h - 1
min은 맨 밑줄이 딱 한개 차있는 2^h - 1 - 2^(h-1) + 1 = 2^(h-1)
만약 맨 밑줄이 다 비면, height이 h라는 처음 조건을 만족 안하니까 1개는 최소로 있어야 해요!
흠..근데 왜 오른쪽부터 몇개 노드가 없는 걸 따로 이름붙였을까?? 이 트리의 의의는 뭐지...?
아직은 모르니까 넘어갈게요!
그리고 height은, n이 전체 노드 갯수일 때,

??뭔소리지...? 수식은 넘흐 어려웡
n이 4라고 하면 위의 공식에서는 h=3이고 밑에서도 3이넹
위공식은 어케 나왂는지 아는데 밑에는 뭘까
6. Skewed Binary Tree
skewed라는 단어의 뜻을 잘 몰랐었는데,

왜곡된, 편향된 이라는 뜻이었네요!
실제로 트리도 그렇게 생겼어요 ㅋㅋㅋㅋㅋㅋㅋㅋ
얘는 Left Skewed Tree인데 실제로 왼쪽으로 왜곡된 모습을 확인할 수 있습니다

이건 Right Skewed Tree...

Skewed Tree는 height과 node수가 똑같은게 특징이래요!!
뭐...직관적으로도 당연하네..!
7. Arbitrary Binary Tree
임의의 이진트리가 있다고 할 때,

n = h면 skewed 형태인거고
n= 2^h -1 이면 full binary tree겠군
h는 당연히 n과 log2(n+1)사이에 있겠당ㅎㅎ
'Algorithm > 이론' 카테고리의 다른 글
| [자료구조] binary tree 복사하는 C코드 (0) | 2019.05.31 |
|---|---|
| [자료구조] 스택 없이 트리를 traverse 하는 법 (0) | 2019.05.31 |
| [자료구조]트리/Binary Tree 탐색(traversal) (0) | 2019.05.28 |
| [자료구조]트리/Binary Tree의 표현 (0) | 2019.05.26 |
| [자료구조]트리/포레스트(forest), forest -> binary tree (0) | 2019.05.22 |
