티스토리 뷰
알고리즘 문제중에 굉장히? 그나마 흥미로운 문제라고 생각했던 knapsack problem!!!!
knapsack은

작은 배낭이라는 뜻이다...귀엽네...
가방에 어떤어떤 물건을 넣을수 있을까? 를 물어보는 알고리즘 문제다.
미국놈들은 이렇게 문제 이름은 귀엽게 짓고, 문제는 ㅈㄴ 어렵게 내는 습관이 있는 것 같다.
아무튼 가방에 어떤 물건을 넣을 수 있을지 dynamic problem으로 풀어보자 ^^

나에게는 이런 4개의 물건이 있다. 각각은 weight과 value를 가지고 있다.
그리고 나에게는 한개의 가방이 있는데, 이 가방에는 최대 7만큼의 weight만 들어갈 수 있다. 내가 넣은 물건들의 value의 합이 최대가 되게 하려면, 어떤 어떤 물건들을 넣어야 할까???
이를 Dynamic programming으로 해결하기 위해서 다음과 같은 표를 만들었다.
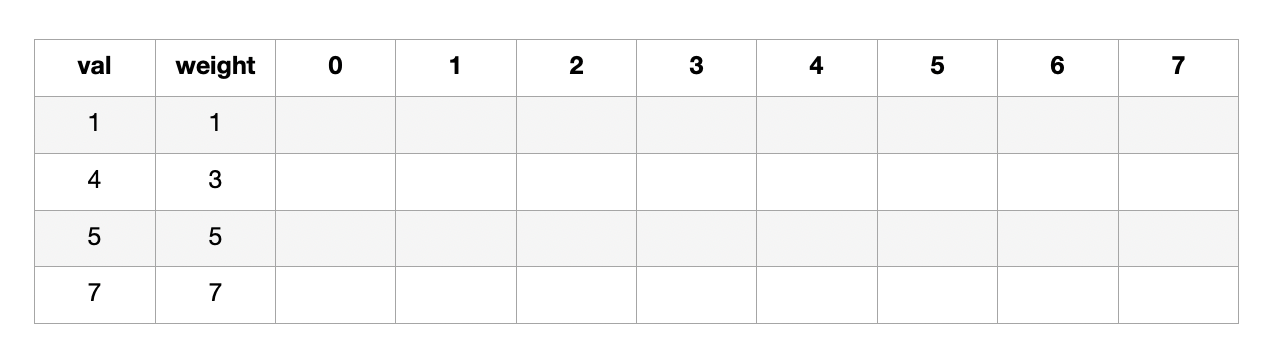
왼쪽 두 세로줄은 4개의 물건에 대한 val, weight이다.
위쪽 0부터 7까지는 total weight이다.
빈 칸에 채워넣을 값은, maximum value이다.

일단, total weight이 0이 될수는 없으니까 전부 다 0으로 채워준다.
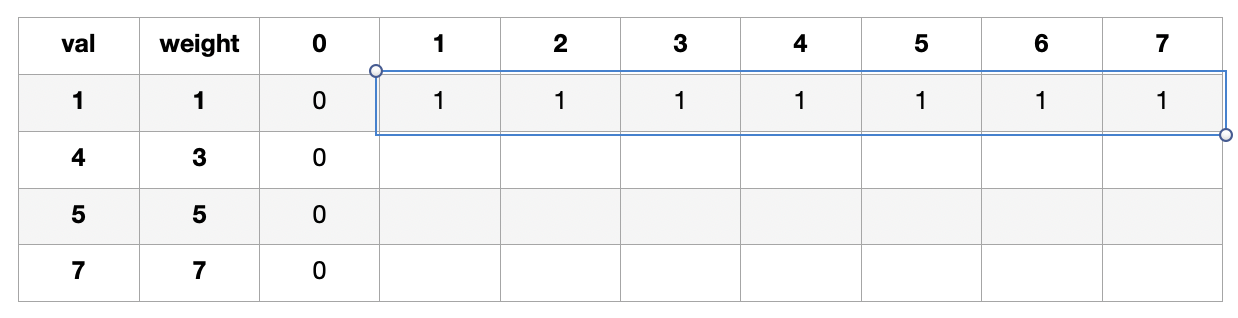
그 다음 total weight이 1이 되려면, maximum value는 1이고, 그 이상의 애들도 여기서는 1밖에 안된다.
다음줄로 가면

3을 포함하고는 total weight이 1,2가 될 수 없으니까 윗줄꺼를 복사해서 온다.

maximum(4 + T[0][0], 1) = 4여서 4를 채워준다. maximum 함수가 키포인트이다!
왜 T[0][0]이냐면, 3-3 하면 0이 남는데 윗줄(0)에서 0번째를 선택하면 T[0][0]이다.

마찬가지로 그 다음칸도, maximum(4 + T[0][1], 1)이라 5가 채워지게 된다.
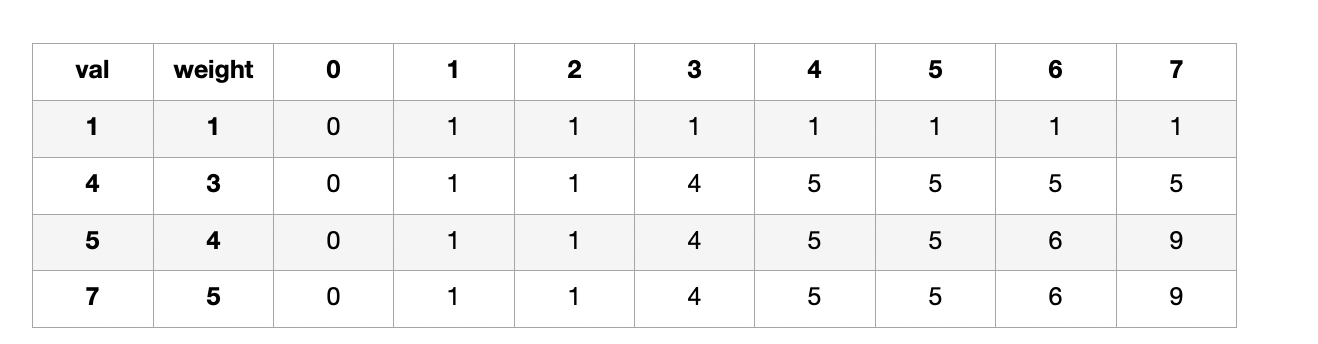
이런식으로 해서 완성!!
윗줄에서 현재 무게 뺀 값 과 윗줄을 max해서 알고리즘이 완성된다.
따라서 제일 큰 값은 9이게 된다.
9에 어떤 어떤 물건이 들어간건지 알고싶으면 다음과 같이 하면 된다.
일단 9가 윗줄과 같은걸 보니 (7,5)인 물건은 안들어간거고... 그 윗줄과 다른걸 보니 (5,4)는 들어간거다.
7-4 = 3이니까 그 줄의 3인 T[1][3]에서 온거고, 걔는 T[0][0]에서 왔다는걸 알 수 있다.
knapsack problem의 코드는 다음과 같다.
def knapSack(W, wt, val, n):
K = [[0 for x in range(W + 1)] for x in range(n + 1)]
# Build table K[][] in bottom up manner
for i in range(n + 1):
for w in range(W + 1):
if i == 0 or w == 0:
K[i][w] = 0
elif wt[i-1] <= w:
K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w])
else:
K[i][w] = K[i-1][w]
return K[n][W]
# Driver program to test above function
val = [60, 100, 120]
wt = [10, 20, 30]
W = 50
n = len(val)
문제를 풀어보고 싶다면 백준 12865 - 평범한가방. 을 추천드립니다
'Algorithm > 이론' 카테고리의 다른 글
| [Algorithm] N-Queens Problem with backtracking (0) | 2020.06.17 |
|---|---|
| [Algorithm] subset sum problem in dynamic programming (0) | 2020.06.17 |
| [Algorithm] 피보나치 수열의 시간 복잡도 (0) | 2020.03.26 |
| [자료구조]다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2019.06.16 |
| [자료구조] 그래프/ DFS(depth-first search) 코드 (0) | 2019.06.10 |
