티스토리 뷰
1. Groups
2. Rings(X)
3. Fields
1. Groups
<G, ·>
* abelian(commutative) group이려면 5가지 만족

2. Field(체)
집합과 두 연산자
<G, ·, ⃞>
<G, ·> 도 abelian이고 <G , ⃞>도 abelian이고, a ⃞ (b·c) = (a ⃞ b)·(a⃞⃞ c)가 성립하면 Field이다.
그런데, 정수들로 이루어진 field가 필요하다. 이게 바로 GF(p), GF(2^n)이다.
Field에 대해서 배웠으니까 이제 Galois Field(갈로아 체)도 다룰 수 있다.
GF(p) = <𝗭p, +, x> 이고 p는 소수이다.
𝗭p = {0, 1, ..., p-1}
그러면 GF(2)를 보자.
GF(2) = < {0, 1}, +, x >이다.
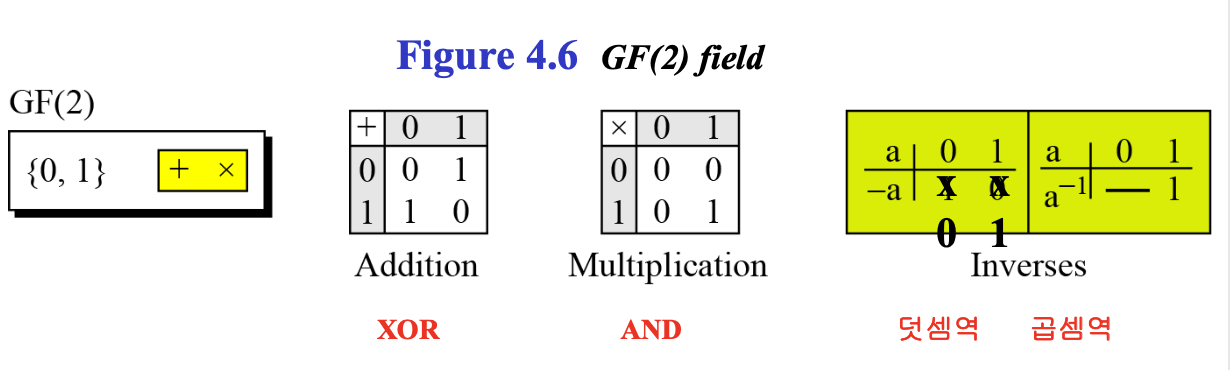
덧셈, 곱셈한 결과에 mod 2를 취해줬다고 생각하면 된다.
GF(2^n)
= {0, ..., 2^n - 1}
2^n이라는건 이진수로 n bit라는 의미이다.
테이블이 어떻게 생겼는지 생각해보자.
1001 1001이라는 다항식은 x^7 + x^4 + x^3 + 1로 바꿀 수 있다.
다항식의 덧셈은 XOR과 같다.
그렇다면 multiplication은 어떻게 될까??

GF(2^8)에서 정의되는 이 두 식을 곱한다면, x^5 * x^7 = x^12 이므로 GF(2^8)에서 넘친다.
그래서 쓰는 개념이 irreducible polynomial(기약다항식) 이다.
기약다항식은 더 낮은 차수의 다항식으로 나눌 수 없는, 즉 인수분해가 안되는 다항식이다.
GF(2^n)에서 곱셈을 정의하려면 최대항이 n차인 기약다항식이 필요하다.

기약다항식의 예시이다.
아까 문제로 들고 온 식을 풀어보자.

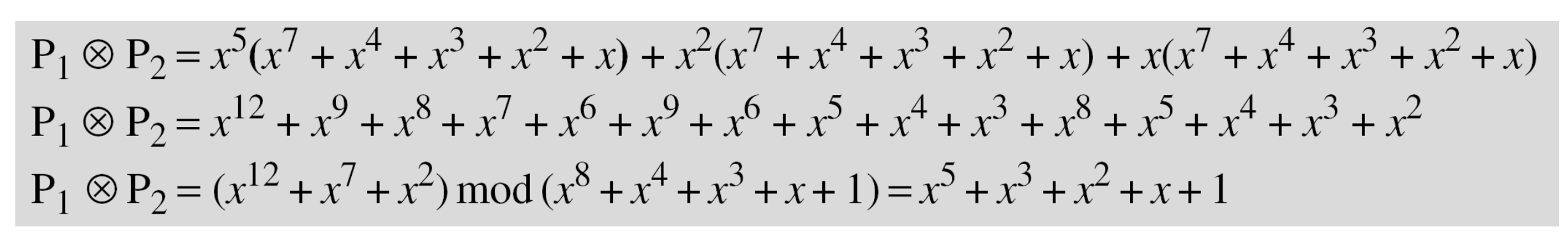
기약다항식 하나를 갖고 mod를 해서 나머지 식만 구한다.
따라서 GF(2^n)을 할때는 어떤 기약다항식을 쓸지 미리 정해야한다! 문제에서도 미리 주어져야 한다.
그러면 곱셈에서의 역은 어떻게 정의할까? 앞서 배운 extended euclidean algorithm을 이용한다.

'정보보안' 카테고리의 다른 글
| [정보보안] Kerckhoff's principle (0) | 2021.04.18 |
|---|---|
| [정보보안] Multiplicative Inverse(곱셈역) (0) | 2021.04.16 |
| [정보보호] AES - Advanced Encryption Standard (0) | 2021.04.13 |
| [정보보안] DES Algorithm (0) | 2021.03.30 |
| [정보보안] Euclidean Algorithm, Extended Euclidean Algorithm (0) | 2021.03.08 |
