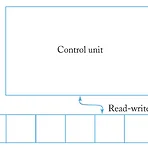
 [Automata] Turing Machine
[Automata] Turing Machine
Chapter 9의 내용이다! automaton의 4가지 부류 Finite-state machine : 간단~ Pushdown automata Linear-bounded automata Turing machine: 복잡~ finite state machine인데 inverse가 true 아니다. 그 중 Turing Machine은 최고 등급의 automaton라고 볼 수 있다. 이 챕터를 배우기 위해서 그동안 오토마타를 배워왔다고 해도 과언이 아닐 만큼... https://namu.wiki/w/튜링%20머신 https://namu.wiki/w/오토마타 꽤 재미있으니까 위 나무위키 문서를 읽어보길 바란다 :) Turing Machine의 정의 Turing Machine M은, M = (Q, Σ, Γ, 𝛿,..
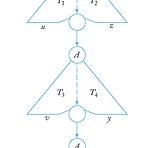 [Automata] CFG와 Pumping Lemma
[Automata] CFG와 Pumping Lemma
Chapter 8의 내용이다! CFG의 특성에 대해서는 이미 정의할 때 한번 다뤘는데 왜 또 얘기하지? 싶었는데 Pumping Lemma를 다루기 위한 것이였던 것 같다! Theorem 8.3, 8.4 CFL은 union, concatenation, star-closure에 닫혀 있다. intersection과 complementation에는 닫혀 있지가 않다. Theorem 8.5 L1이 context free language이고 L2이 regular language라면 L1 교집합 L2는 context free이다. Theorem 8.6 Context-free grammar G=(V, T, S, P)에 대하여, L(G)가 비어있는지 아닌지를 결정하는 알고리즘이 있다. Theorem 8.7 Contex..
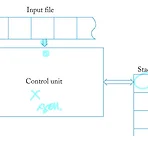 [Automata] Pushdown Automata
[Automata] Pushdown Automata
Chapter 7의 내용이다! 일단 Pushdown Automata와 그 전의 automata와 가장 크게 다른 점은 pushdown automata는 스택을 사용할 수 있다는 것이다! Nondeterministic Pushdown Automata Pushdown Automata의 정의 M = (Q, Σ, Γ, 𝛿, q_0, z, F) * Γ 은 감마라고 부른다. 잘 보면 기존에 배웠던 finite automata에서 2가지의 원소가 추가되었다. 바로 Γ 와 z이다. Q: control unit의 initernal state의 유한 집합Σ: input alphabet Γ: 유한한 개수의 집합인 stack alphabet 𝛿: Q X ( Σ sum {ƛ}) X Γ : transifion function이 ..
Chapter6의 내용이다! 앞서 배운 문맥자유문법 같은 경우, 우변에 오는 형태에 어떠한 제약도 없었다. 그런데 이게 항상 좋기만 한것도 아니다.. 따라서 이번 챕터에서는 문법을 단순하게 만드는 방법에 대해서 다뤄보려고 한다. 하지만 단순화 한다고 해서 무조건! 개수가 줄어야 하는 것이 아니라는걸 염두에 두자. 유용한 치환 규칙 어렵지 않은 규칙이다. A->aB B->c라면 A->ac로 바꿀 수 있다는 규칙이다. 증명은 생략하겠다. 필요없는 production 삭제하기 먼저 변수가 필요없다와 필요 있다를 구분하는 방법을 알아야 하는데, (Definition 6.1) 필요 있다 : L(G)에 포함되는 w에 대하여, S->xAy->w 으로 만들어질 수 있는 x, y가 (V set T)* 에 대하여 w가 하..
 [Automata] Context-free Language ( 문맥 자유 언어 )
[Automata] Context-free Language ( 문맥 자유 언어 )
Chapter 5의 내용이다! 이전 포스팅에서 다뤘듯이 정규언어가 좋긴 한데, 프로그래밍 언어를 다루기에는 조금 부족한 요소들이 있었다. L = {a^n b^n: n>=0} 이면, a=(, b=)일 때 프로그래밍에서 괄호가 중첩인지 확인하기 좋지만 얘 역시 정규언어가 아니였다. (정규언어가 아님은 펌핑lemma를 통해서 보였다.) 따라서 우리는 정규언어보다 더 큰 개념인 '문맥 자유 언어'를 다룬다. 정규언어의 큰 단점은, 좌변은 한개의 변수이고 우변은 특정한 형태여야 했다. (정의임) 문맥 자유언어는 우변에 특정한 형태 대신 아무거나 올 수 있게 허용해줌으로써 더 강력해진다!! 정규언어 ⊂ 문맥 자유 언어이다. * linear grammar? 문제들은 주로, 주어진 언어가 문맥자유언어인지 보이라는 유형..
chapter 4의 내용이다! 정규 언어의 Closure 정규 언어에 대한 주요한 질문들 비정규 언어 판별하기 - pigeonhole principle(비둘기집 원리) 예시로 살펴보자! L = {a^n b^n: n>=0} 이면 L은 정규언어일까? (예제 4.6) 여기에 해당하는 언어는 L = { ƛ, ab, aabb, ... } 등이 있을 것이다. 이 문제를 귀류법으로 접근하면, L이 regular language라면 DFA M = {Q, {a,b}, 𝛿, q_0, F}가 존재할 것이다. i=1,2,3..일 때 𝛿*(q_0, a^i)를 생각하면 i는 무한대로 많을 것인데 M에는 state개수가 유한하다. 그렇다면, 𝛿*(q_0, a^n) = q 𝛿*(q_0, a^m) = q인 서로 다른 n, m이 존재하..
 [Automata][WIP] 정규 언어와 정규 문법
[Automata][WIP] 정규 언어와 정규 문법
이번에는 chapter 3의 내용을 다루려고 한다!.! 정규 표현식 ( Regular Expression ) 정규표현식은 알파벳, 덧셈(+), 곱셈(·), 제곱(*)으로만 이루어져 있다. 덧셈 a+b는 a랑 b로 이루어진 집합에서 뽑아서 쓰는 것이다. a+b = {a, b} 라고 생각하자. 제곱 (a+b)*는 ƛ, a, b, aa, ab, ba, bb, aaa ,,, 등이다. 순서 상관 없다! a*는 0개 이상 반복이다. 예1 ) r = (a+b)*(a+bb) 예2) r = (aa)*(bb)*b 정규 표현식과 정규 언어의 관계 정규 문법 ( Regular Grammar ) 예1) V_0 -> aV_1 V_1 -> abV_0 | b V_0이 시작임
Automata 이론이란? abstract한 computing device에 대한 공부이다. automaton : abstract computing device 다룰 내용 Introduction to the Theory of Computation Mathematical Preliminaries and Notation Finite Automata Deterministic/Non-Deterministic Finite Accepters Regular Languages and Regular Grammars Properties of Regular Language Context-Free Languages Simplification of Context-Free Grammars and Normal Forms Pushd..
 [Automata][WIP] Finite Automata - DFA, NFA
[Automata][WIP] Finite Automata - DFA, NFA
이번 포스팅에서는 Chapter 2의 내용을 다뤄보려고 한다. Deterministic Automata: 현재 상태에 의해서 move가 결정된다. Nondeterministic Automata: 여러개의 move가 있을 수 있다. DFA(Deterministic Finite Accepters): 결정적 유한 인식기 특징 내부 상태 개수가 유한하다. input string은 심볼의 sequnce로 구성됨 한 state에서 다른 state로 transition 가능 output이 있다 DFA의 정의 (1) DFA는 다음과 같은 5개 원소의 tuple로 정의된다. M = (Q, Σ, 𝛿, q0, F) Q: 유한개의 internal state의 집합 Σ: input alphabet 𝛿: Q ✖️Σ -> Q 는 ..
이번 포스팅에서는 Chapter 1의 내용을 다뤄보려고 한다! Chapter 1 답게 기본 상식들이 많이 나와서 이미 아는 부분들은 생략 했다. Introduction to the Theory of Computation에서는 증명 방법 - induction(귀납법), contradiction(귀류법) 내용이 간단하게 나오지만 Language, Grammar, Automaton이 이 단원의 포인트라서 이 부분만 집중적으로 다뤄보려고 한다. Languages string의 집합! string = {a, b, c, ...} 라면 string으로 만든 aa, bb, ccc, 등의 문자열이 language이다. Reverse: 거꾸로 string= {a, b}라면 {a, b, aa, bb, ab, ...} 등 0..
