티스토리 뷰
Elliptic Curve CryptionSystem은 keysize가 엄청 작은 장점이 있다!!!!
일단 타원곡선은

형태로 정의되는 곡선이다.
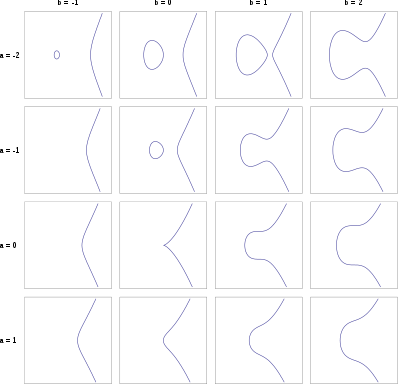
이런식으로 생김...
특징은, 4a^3+27b^2 ≠0 이어야 하는데, 식이 실근,허근 상관 없이 3개의 근을 가져야 하기 때문이다.

일단 이 점들의 집합에 대해서도 + 부호에 대해서 Abelian Group을 채택하고 싶어한다.
아벨 군의 조건은 다음과 같다.

예를 들어, E = {(x,y) | y^2 = x^3 - 4x} 라는 타원 곡선 위의 모든 점의 집합을 정의해보자.
Operation (+): 점 덧셈 (point addition)
아벨군을 +연산에 대해서 정의하는걸 시도해보자.
위에서 제시한 조건들 중, 4번인 Identity는 (0,0)이나 무한대인 점을 사용한다.
5번인 역은 y부호만 바꾸는걸로 해서 정의한다. P = (x,y)였으면 -P = (x, -y)로 정의한다.
근데 덧셈 자체를 어떻게 정의해야 할까?
일단 크게 3가지 경우로 나누어서 본다.

두개의 서로 다른 점을 더할 때, P, Q에 선을 그어서 R을 찾는다.
타원곡선은 근을 세개 갖기 때문에 무조건 또 다른 한 점에서 만난다.
그 만나는 점에서, y부호가 반대인 점을 R로 정의한다.
계산은 어떻게 할까?
람다(ƛ)를 P, Q를 지나는 직선의 기울기라고 정의한다.
P = (x1, y1)
Q = (x2, y2)라고 하면,
ƛ = (y2-y1) / (x2-x1)
따라서 ℓ의 식은 y = ƛx + β
근데 곡선의 식은 y^2 = x^3 + ax + b였으니까,
두 식을 연립한다.
계산결과는,
x3 = ƛ^2 -x1 - x2
y3 = ƛ(x1-x3) - y1
inverse는 p=17이었으면 (4,2) -> (4,11)같이 된다.
덧셈 역시 GF(p)에서 계산하면 된다.
같은 점을 두번 더하려면 어떻게 해야 할까?
위 그림처럼 계산해준다.
방식은 위와 같아서 생략
람다 = (3x1^2 + a) / 2y1 mod p
x3 = 람다^2 -2x1 mod p
y3 = 람다(x1-x3) - y1 mod p
E, +가 아벨군인지 확인해본다.

잘 성립하는것을 볼 수 있다!!
GF(p)에서 타원 곡선 적용하기
위에서는 모든 실수 점에서 다뤘다.
근데 일반 실수 점은 암호학에서 이용하기가 어려우니까 GF(p)에서 적용하기 시작한다.
양쪽에 mod p만 취해주면 된다.
y^2 mod p = (x^3 + ax + b) mod p

(4,2)의 덧셈역은, mod p상에서 연산이 이루어지기 때문에 (4,11)이다. 그래서 처음 그래프와는 위치가 달라질 수 있다.
키 생성하기
공개키: e1, e2, p, a, b
개인키: d
(1) GF(p)를 할 p 정의, Ep(a,b)인 점 고르기.
(2) Ep(a,b)에 들어있는 e1: (x1, y1) 점 선택하기
(3) d 선택
(4) e2 = (x2, y2) = d*e1
암호
Ep(a,b)에 포함된 P(PlainText)를 고른다. 이게 plainText임. (텍스트를 점으로 변환하는 방법에 대해서는 다루지 않는다.)
양수인 정수 r 선택.
C1 = r * e1
C2 = P + r * e2
복호
P = C2 - (d*C1)
예제
1. 키 생성

2. 암호

3. 복호

Elliptic Curve Discrete Logarithm Problem
e2 = d * e1
d, e1을 알고 e2를 계산하는건 쉬운데
e1, e2로 부터 d를 계산하는건 매우 어렵다. 이게 ECDLP!
'정보보안' 카테고리의 다른 글
| [정보보안] 모듈로 계산의 성질 (modular) (0) | 2021.06.10 |
|---|---|
| [정보보안] Cardinality of Primes - 소수의 무한성 증명하기 (0) | 2021.06.10 |
| [정보보안] ElGamal 공개키 암호 (0) | 2021.05.25 |
| [정보보호] 페르마의 소정리 ( Fermat's Little Theorem ) (0) | 2021.05.03 |
| [정보보안] Autokey, Playfair, Vigenere, Hill Cipher, One-Time Pad (0) | 2021.04.18 |
