sweetdev

Forest로 시작한다. 장점 : 트리가 여러개 나올 수 있다.

트리를 만들기 위한 시작 노드를 하나 지정하고(어떤 노드여도 괜찮다), 그 노드에 minimum cost edge를 더해준다. 만약 노드를 더하는데, 이미 있는 노드 두개로 만들게 되는 edge라면 더하지 않는다.

* greedy algorithm을 따른다 * minimum cost spanning tree를 얻기 위한 과정 * 과정 1. edge를 다 지운다 2. 제일 cost가 작은 edge를 하나 더해준다 3. Q) global optimum을 얻지 못할 수도 있지 않을까? A) 항상 global optimum을 얻을 수 있다는 것이 증명되었다. 교재에 proof 있음

Binary search tree는 탐색, 삽입, 삭제, 연산에 있어서 지금까지 공부했던 어떤 자료구조보다도 성능이 좋다고 한다!! 열심히 공부할 이유가 되는군!! [Definition] (1) 모든 원소는 키를 가지며, 어떤 두 원소도 동일한 키를 갖지 않는다 (2) 왼쪽 subtree에 있는 키들은 루트의 키보다 작다 (3) 오른쪽 subtree에 있는 키들은 루트의 키보다 작다 (4) 왼쪽, 오른쪽 subtree도 모두 binary search tree이다. BST(binary search tree, 앞으로는 BST라고 부를게요) 의 가장 큰 특징은, inorder로 traverse했을 때 작은 순서대로 라는것 !!

이렇게 생긴 max heap에서 root인 50을 지운다고 해 보자. 우리가 쓰는 알고리즘은 가장 오른쪽에 있던 값을 떼서 루트에 넣고 본다.(대책 노...) 이제 adjust를 하는데, 31이랑 49랑 바꿔본다. 31이랑 또 48이랑 바꾼다. 이러면 다시 max heap의 조건을 충족한다. 근데 바꾸는 기준이 뭘까?? 44랑 바꿔도 max heap은 됐는데...? 이건 코드를 보면 알 수 있다. //코드가 정말 보기싫다. 다음에 정리하자

이런 max heap에서 원소 하나를 삽입한다고 해 보자. complete binary tree의 조건을 만족하려면, 원소 하나가 들어갔을 때 트리는 무조건 저 자리에 들어갈 수 밖에 없다. 삽입되는 원소의 정확한 위치를 결정하기 위해서는, 트리의 새 노드에서 시작해서 루트 쪽으로 올라가는 bubbling-up 방법을 사용하면 된다고 한다. 삽입되는 원소는 삽입이 완료된 뒤, 최대 힙이 되는 것이 확인될 때 까지 위쪽으로 계속 올라간다. 예를 들어서 생각해보자! 새로운 원소가 30이라면, 바로 저 자리에 넣으면 된다. 그러나 값이 49이면 넣을 수 없다. 그러므로 31을 검은색 위치에 넣고, 최대 힙이 되는지 본다. 여전히 안 된다. 그럼 48을 그 자리에 넣는다. 여전히 안된다. 51을 그 자리에 넣는..

1. priority queue란? 우선순위 큐에서는 우선순위가 가장 높은, (또는 낮은) 원소를 먼저 삭제한다고 하고, 임의의 우선순위를 가진 원소를 우선순위 큐에 삽입할 수 있다고 합니다. FIFO인 일반 큐와는, 우선순위 순서로 pop하는 기능이 다릅니다. 우선순위 큐가 왜 필요하냐면, 똑같은 기계를 쓰는 소비자 중에 3000원을 낼 사람, 1000원을 낼 사람, 2000원을 낼 사람이 있다고 하면 기계는 3000원을 낼 사람을 먼저 쓰게 해주고, 그 다음 2000원, 그 다음 1000원을 낼 사람 순으로 써주게 하는 것이 가게 주인 입장에서 최고이죠? 이런식으로 큐에 넣는 원소들에 우선순위를 부과해야 할 때, 우선순위 큐를 쓰면 됩니다. 이 경우는 max priority queue이고, 반대 경우..

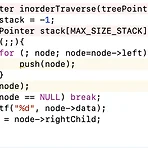
https://sweetdev.tistory.com/120 불러오는 중입니다... 이 글에서 '스택 없이 트리를 traverse 하는 법에 threaded binary tree를 쓰는 방법'이 있다고 했는데, 오늘은 그 방법에 대해서 다뤄보려고 한다. binary tree에서는 inorder traverse 하기 위해서 스택을 썼었다. (이제 혼자서도 잘짜요!..ㅎㅎ) 그럼, threaded binary tree에서는 어떻게 구현할까?? 이렇게 구현하면 된다고 한다.

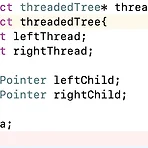
쓰레드라는 표현을 굉장히 자주 들었는데 뭔지는 몰랐었다. 여기서 살펴보고자 한다! binary tree의 링크 표현을 보면, 실제 표현보다 더 많은 null link가 있다고 한다. 이진 트리에는 총 2n개의 링크 중에 n+1개의 null link가 있으니까, 과반수 이상이 놀고있는 링크인 것이다. 이것을 안타까워한 어떤 공머생이, null link를 Thread라는, 다른 노드를 가리키는 포인터로 대치하였다고 한다. 규칙은 다음과 같다 (1) ptr-> leftChild가 null이면, ptr-> leftChild를 inorder traverse 할 때, ptr 앞에 방문하는 노드에 대한 포인터로 대치한다. 이것은 null link를 ptr의 inorder predecessor에 대한 포인터로 대치하는..

명제 해석 식에 대한 만족성 문제는, 식의 값이 true가 되게 지정할 수 있는 방법이 있는지를 묻는 문제라고 한다. 책의 설명을 보니 되게 중요한 문제인가보다. 1950년대에 휴리스틱 프로그래밍의 가능성을 증명하기 위해서 썼다고 한다. 잘 모르겠어서 여기까지만 쓴다 ^^;;

copy코드와 비슷하게, 재귀로 짰다

재귀를 이용해서 짜면 쉽다! leftChild, rightChild, data이케 해버리면 개꿀

스택 없이 트리를 traverse 하는 방법이 있다고 한다. 각 노드에 parent field를 추가하면 된다는데...? 이렇게 하면 한 노드에서 루트 노드로 올라가고 다시 밑으로 내려올 수 있다고 한다. 또 다른 해결책은 이진트리를 쓰레드 이진 트리로 표현하면 된다고 한다. ???

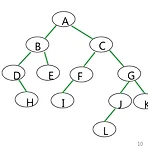
이것도 이산수학에서 배운 내용이긴 한데, 기억이 가물가물하고 그때는 벼락치기 했으니까 다시 정리해볼게요!! Preorder Traversal Inorder Traversal Postorder Traversal 그리고 Levelorder Traversal 이케 세가지를 배울거라고 합니다 Preorder: 이름처럼, 자기 자신(root)-left-right Inorder: left-root-right Postorder: left-right-root 이렇게 생긴 바이너리 트리가 있다고 해 봅시다! 얘를 preorder, inorder, postorder로 traverse 해보아용 preorder: A-B-D-H-E-C-F-I-G-J-L-K inorder: D-H-B-E-A-I-F-C-L-J-G-K postor..

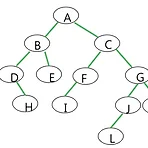
Array로 표현하기 이렇게 생긴 트리를 Array로 표현하려고 하면, 요런식으로 표현해서 넣는다고 한다! 왜 0번에는 아무것도 안넣었을까?? 나중에 쓰나!? 궁금하지만 역시 아직 모르니까 pass... Array[i]번째에 있는 Node는, 걔의 left child는 Array[2*i]에, right child는 Array[2*i + 1]에, Parent는 Array[(i/2)의 내림] 에 있다고 한다 i에 6을 넣어서 확인해보면, 6번째 칸에는 F가 있고 걔의 left child는 I, right child는 없음, parent는 C인데 과연 맞을까?! 12번째 칸 = I 13번째 칸 = 없음 3번째 칸 = C 다 맞다 ㅎㅎ Node로 표현하기 아까 그 그래프를 Node로 표현하면, Node 구조를 ..

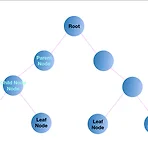
안녕하세요 SweetDev입니다. 저는 지금 컴공 2학년 수업인 자료구조에서 트리를 배우는 중이라고 해서(사실 수업 잘 안가서 모름) 시험공부도 미리 할 겸 트리를 정리해보려고 합니다! 1. 정의 트리 : hierarchy구조의 데이터를 표현하기 위한 자료 구조 2. 트리를 표현하기 위해서 쓰는 단어들 Node Root Node Child Node , Children degree, fan out Sibling Ancestor Descendant Leaf node, Leaves, Non-Leaf Node Subtree Forest Path from node x to node y Level 0, 1, 2, ~ h-1 1, 2, 3, ~ h Height : max, level 이런 단어들을 배울 예정이라고 하..

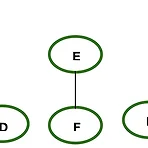
[정의] forest는 n개의 disjoint tree의 집합이다 나무가 모이면 숲이 되듯, tree가 여러개 모이면 forest라고 부른다. forest는 tree의 개념과 매우 유사한데, 이는 '트리에서 루트를 제거하면 포리스트가 되기 때문'이라고 한다??? ㅇㅎㅇㅎ...원래 이렇게 생긴 거였구나... 다음 단원에서 'disjoint set'을 표현하기 위해서 forest를 사용할것이라고 한다. [forest를 binary tree로 변환하기] 1. forest에 있는 각 트리를 이진트리로 변환한다. 2. 변환된 모든 binary tree를 root node의 rightChild 필드를 통해 연결한다. 그러면... 요렇게 된다.(아직 그림 안넣음) 이 변환은 이렇게 정의할 수 있다고 한다. Tree1..