[MachineLearning] Activation Function - Step, Sigmoid, ReLU

"밑바닥부터 시작하는 딥러닝"을 읽고 작성한 게시글입니다. 

이 포스팅 에서 퍼셉트론을 다룰 때, 퍼셉트론을 다음과 같은 함수로 정의했다. 

\begin{equation*}
y=\begin{cases}
0\quad (w_1x_1+w_2x_2+b\leq0)\\
1\quad (w_1x_1+w_2x_2+b>0)
\end{cases}
\end{equation*}

 

임계값을 경계로 출력이 바뀌는 이 함수는, 계단같이 생겨서 계단 함수이다. 

Perceptron에서는 Activation Function(활성화 함수)으로 계단 함수를 사용하는 것이다. 

그렇지만 계단함수 외에 다양한 함수들을 사용할 수 있는데, 이 포스팅에서는 새로운 함수로 Sigmoid와 ReLU를 다뤄보려 한다. 

 

1. Sigmoid Function

 

 

 

$h(x) = \frac{1}{1+exp(-x)}$

 

Step Function보다 훨씬 매끈한 것을 볼 수 있다. 이것이 학습에서 중요한 역할을 하는 성질이다. 

 

2. ReLU Function

 

Rectified Linear Unit이라는 의미의 ReLU함수는, 0이 넘으면 그 입력을 그대로 출력하고 0이하면 0을 출력하는 함수이다. 최근에 가장 많이 쓰이는 Activation Function이다. 

 

 

 

 

그 외 이런 함수들이 있다.

 

 

Softplus함수

https://www.google.com/url?sa=i&url=http%3A%2F%2Fm.blog.naver.com%2Fwideeyed%2F221410558037&psig=AOvVaw1Q_W8kkNUCA1LJVYTIWurt&ust=1630482409356000&source=images&cd=vfe&ved=0CAsQjRxqFwoTCKiz4rji2vICFQAAAAAdAAAAABAD

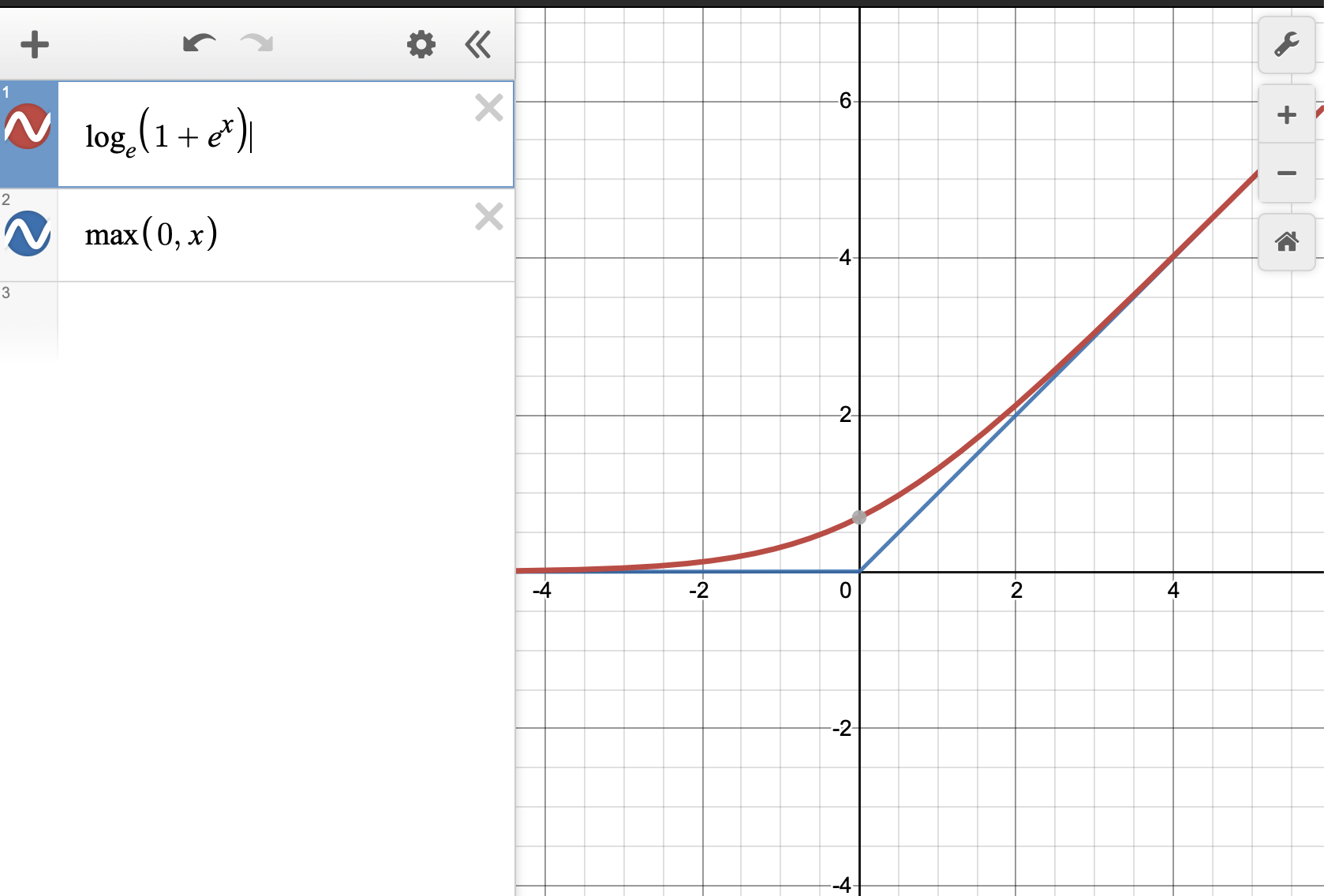
y = log(1+e^x) 

여기서 말하는 로그는 밑이 e인 로그이다. ln이라고 생각해야 함!